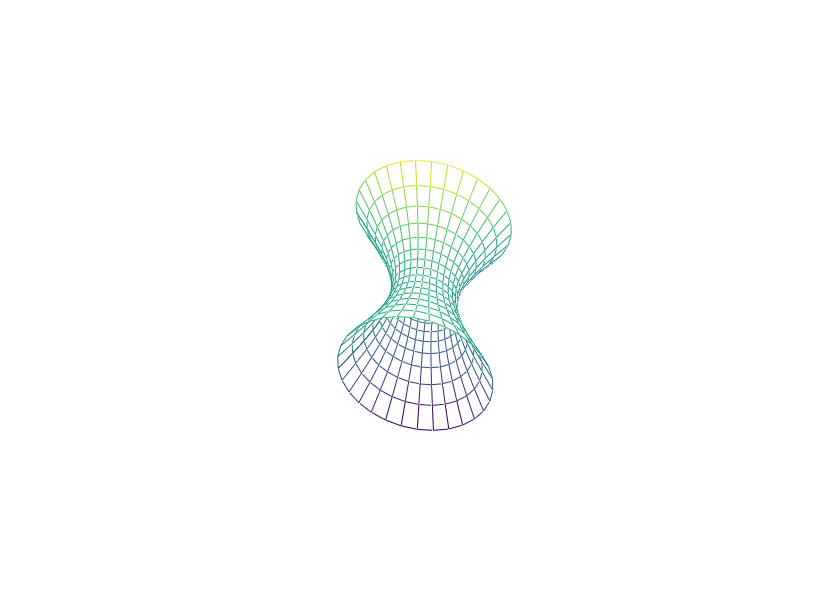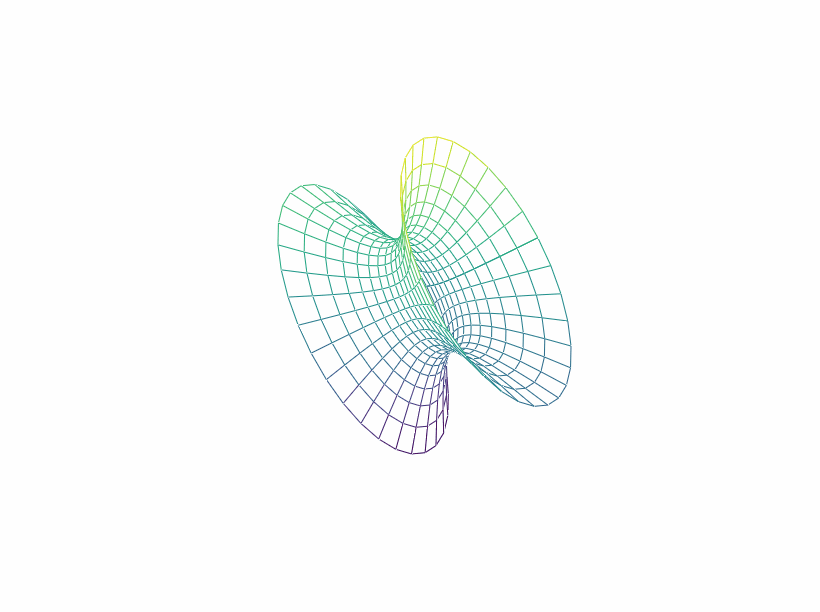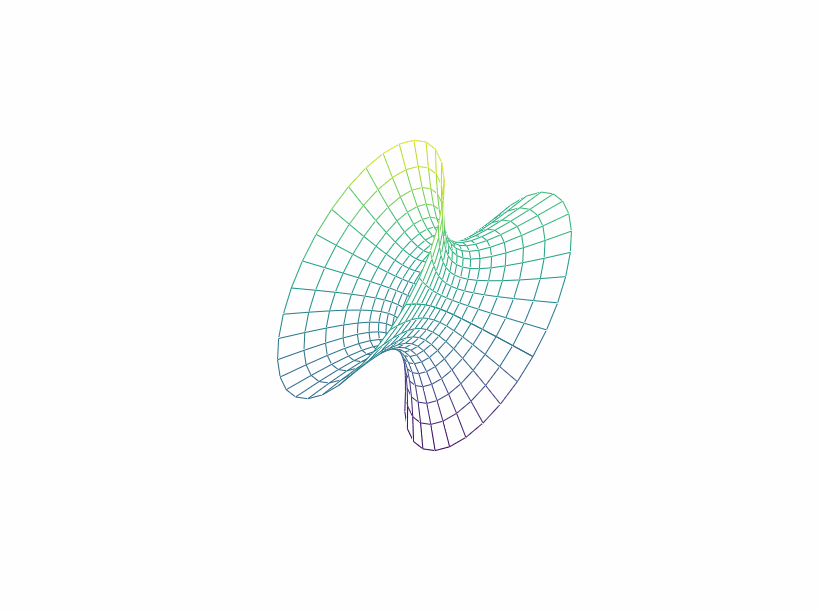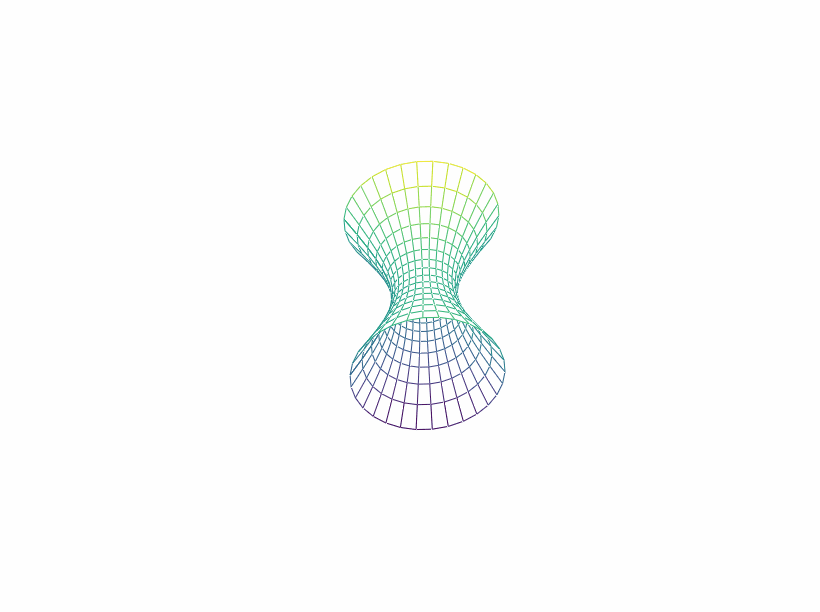 \[
x^2+y^2-4xy-2yz-2zx+2x+4y-10z+27=0
\]
\[
\frac{9}{2}x''^2+\frac{3}{2}y''^2-3z''^2-1=0
\]
\[
x^2+y^2-4xy-2yz-2zx+2x+4y-10z+27=0
\]
\[
\frac{9}{2}x''^2+\frac{3}{2}y''^2-3z''^2-1=0
\]
function itiyousoukyokuB(aa,T,Q)
n=15;
p=0:pi/n:2*pi;
t=(-3/2:3/n:3/2)';
ct=cosh(t);st=sinh(t);
cp=cos(p);sp=sin(p);
a1=1/sqrt(aa(1));a2=1/sqrt(aa(2));a3=1/sqrt(-aa(3));
xxx=a1*ct*cp;
yyy=a2*ct*sp;
yoko=ones(1,2*n+1);
zzz=a3*st*yoko;
for i=1:n+1
xxxx=T*Q*[xxx(i,:);yyy(i,:);zzz(i,:);yoko];
x(i,:)=xxxx(1,:);y(i,:)=xxxx(2,:);z(i,:)=xxxx(3,:);
end
mesh(x,y,z)
axis equal
grid on
end
ax=1;ay=1;az=0;hxy=-2;hyz=-1;hzx=-1;bx=1;by=2;bz=-5;c=27; % hyperboloid of one sheet
%ax=1;ay=-1;az=1;hxy=-1;hyz=-1;hzx=-1;bx=-1;by=-1;bz=-1;c=-5; % hyperboloid of one sheet
%ax=1;ay=-1;az=1;hxy=-1;hyz=-1;hzx=0;bx=-1;by=1;bz=-1;c=-5; % hyperboloid of one sheet
%ax=1;ay=1;az=0;hxy=-2;hyz=-1;hzx=-1;bx=0;by=0;bz=0;c=-6; % hyperboloid of one sheet
%ax=1;ay=1;az=0;hxy=-2;hyz=-1;hzx=-1;bx=2;by=0;bz=-2;c=3; % hyperboloid of one sheet
%ax=1;ay=-3;az=-3;hxy=0;hyz=1;hzx=0;bx=0;by=2;bz=-2;c=-1; % hyperboloid of one sheet
A=[ax hxy hzx;hxy ay hyz;hzx hyz az];
b=[bx;by;bz];
B=[A b;b' c];
[P AA]=eig(A);
aa=diag(AA);
x0=A\b;
T=[eye(3) -x0;zeros(1,3) 1];
Q=[P zeros(3,1);zeros(1,3) 1];
BBB=Q'*T'*B*T*Q;
aa=-aa/BBB(4,4);
if aa(1)<0
R=[0 0 1;0 1 0;1 0 0];
aa=R*aa;
Q(1:3,1:3)=Q(1:3,1:3)*R;
elseif aa(2)<0
R=[1 0 0;0 0 1;0 1 0];
aa=R*aa;
Q(1:3,1:3)=Q(1:3,1:3)*R;
end
itiyousoukyokuB(aa,T,Q)
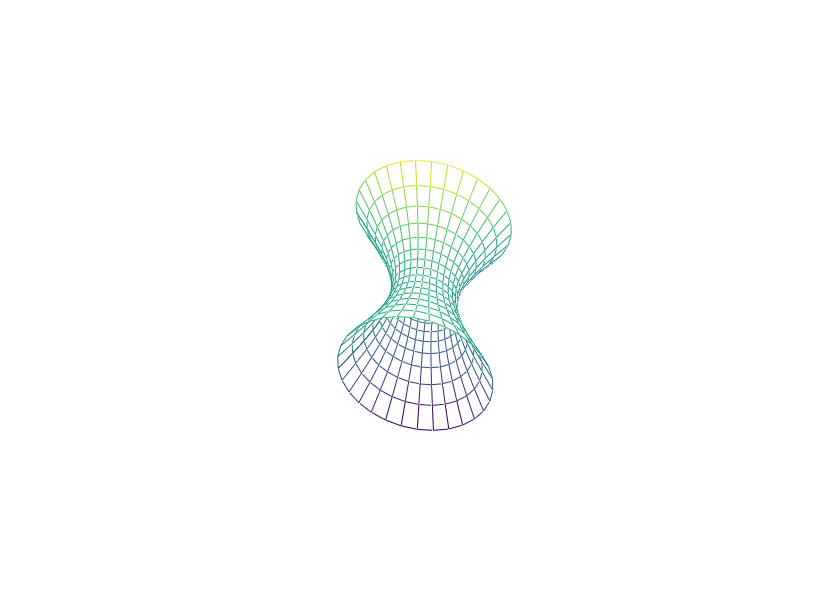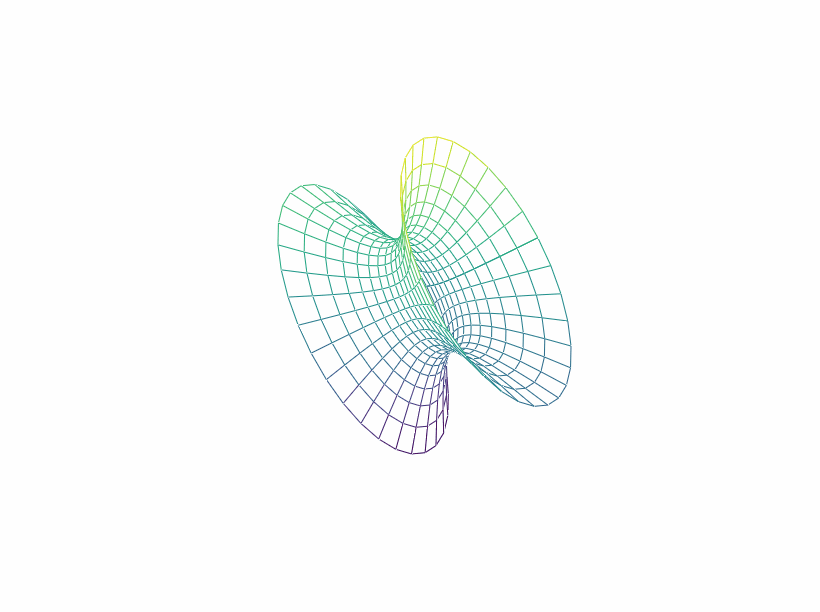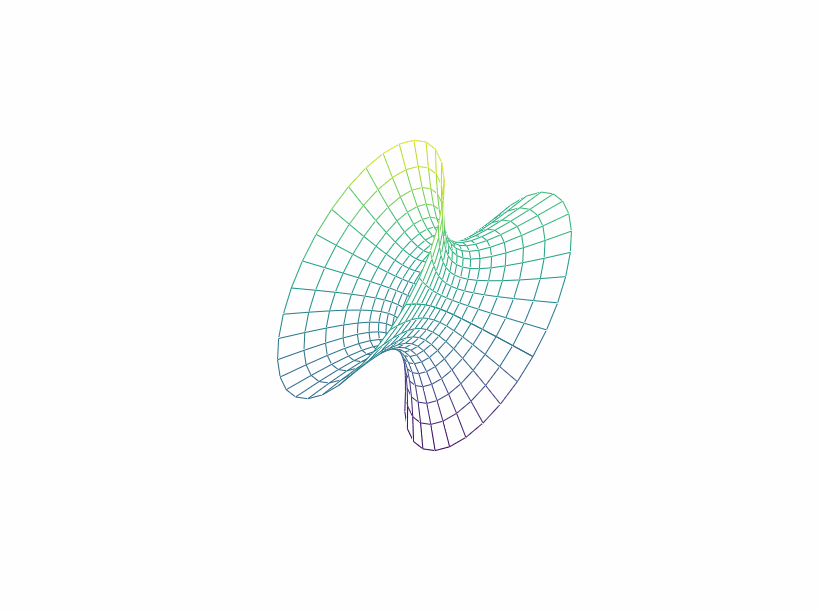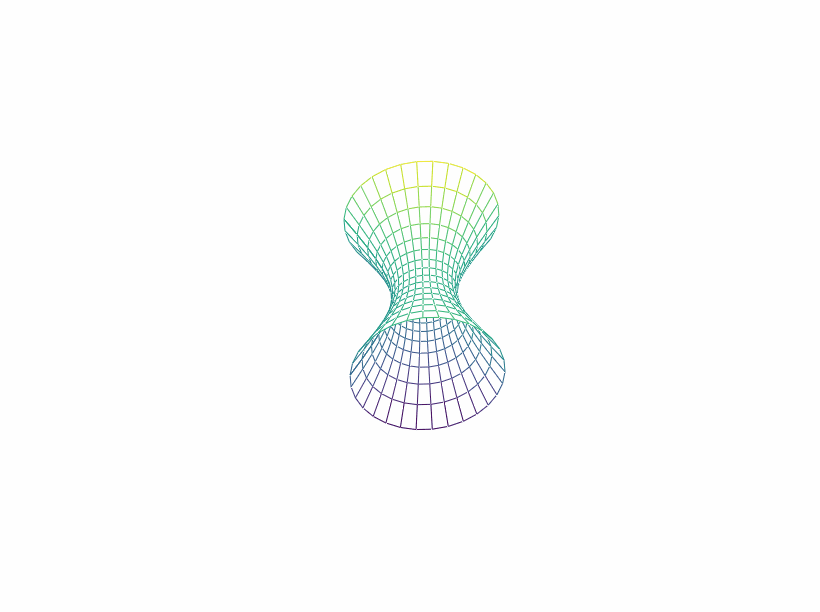 \[
x^2+y^2-4xy-2yz-2zx+2x+4y-10z+27=0
\]
\[
\frac{9}{2}x''^2+\frac{3}{2}y''^2-3z''^2-1=0
\]
\[
x^2+y^2-4xy-2yz-2zx+2x+4y-10z+27=0
\]
\[
\frac{9}{2}x''^2+\frac{3}{2}y''^2-3z''^2-1=0
\]